No way this is going to be a short post, because people have a mistaken fixation on zero, such as: "I'll wait until my returns get back to zero before selling, that way I won't have lost anything."
Similar fixation with zero with respect to volatility and correlation. Volatility is variation about the mean return, not around zero. So two assets could have perfectly inverse (negative) correlation - as differentiated from being uncorrelated - and still both could always be rising.
Even if one chooses to be lax with wording and use "uncorrelated" to mean negatively correlated, this shows that when everything else is going up, an "uncorrelated" (negatively correlated) asset does not need to be going down. It could just be rising less than its mean (average) Thus, it is not mathematically true that "When everything (stocks, bonds, REITs, and more) rises in synch in a bull market, then [an "uncorrelated" asset] must necessarily [go down]".
Say you have two investments, one which rises 1% a month, give or take volatility, and another which rises 1% a month, give or take its volatility. They could have perfect negative correlation. One might rise (in percent) 1 + sin(month #), while the other might rise 1 - sin(month #). These assets move in perfect (inverse) unison. They both rise every month (since sin(x) ≤1), but when one zigs (rises faster than its mean), the other zags (rises slow than its mean).
Why am I going through all this detail? Because aside from revisiting what I tried to explain before, you asked about stocks and bonds. Bonds, on average, rise in every part of the business cycle. So if one looks only at whether an asset class is simply rising or falling (and not looking at how it's performing relative to its mean performance), one would conclude say that bonds must be closely correlated with cash - they both rise together. But that would be wrong. Cash doesn't correlate well with anything, including bonds.
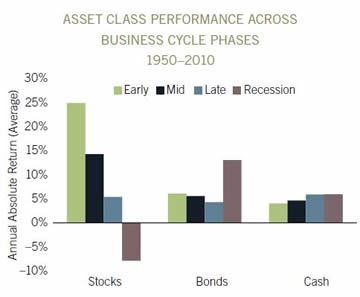
The graph above is from a good Fidelity page on "
How to invest using the business cycle". Stocks and bonds tend to be phase shifted, much like sin and cos, but not as cleanly. So while the correlation coefficient between stocks and bonds tends to be a low (positive) number, it doesn't mean that the performance of stocks and bonds is unrelated. (Nor does it mean that when stocks zig up, bonds will zag down, just that they may gain less than their average.)
Which gets us to Vanguard's precise statement that uncorrelated means that one would expect no systematic linear relationship.
First, linear. As I've been stating, a simple phase shift can produce two curves (say, stocks and bonds) with little
linear relationship (like sin and cos). But they're hardly unrelated. Checking for phase shifts, autocorrelation, etc. is one of the first things one does in looking for patterns in time sequence data.
The word you're more concerned about is "expected". A thing with random variables is that the unexpected happens. It must, else the variables are not random. Toss a fair coin enough times and you will come up with ten heads in a row. Toss two coins (to represent stocks and bonds), and sooner or later they'll match 10 times, 20 times, however many times you choose, in a row.
In short, zero correlation does not imply independence, and independence does not mean variables
must not show correlation over any arbitrary stretch of time (just that they're expected not to).
"zero correlation and uncorrelated synonymous, sure. Not worth using the term about in the first place. "
I think you missed the point of the bolded sentence, viz. that zero correlated (i.e. uncorrelated) assets
don't move together at all. That directly contradicts the claim that an "uncorrelated asset is one that does the opposite".
I agree with you that, unlike the other terms above which have clear mathematical meanings, "reliably" (and hence "unreliably") are weak (vague) words. Outside of this thread, I don't think there's any question that these are extremely fuzzy terms.
"Unreliably" didn't come from a citation. I used the negation ("unreliably") of the word you introduced ("reliably"). Here, I took it on faith that you had some meaning in mind when writing "reliably". I tried to make sense of it, and used it accordingly.
Cash in the "actual investing world". Again, I tried to follow your lead. You suggested looking at how terms are used in journalistic idiom.
We can start with the term "riskless investment". As already discussed, "riskless" entails essentially zero volatility, and cash is the only asset that has that attribute (90 day treasuries, the
usual benchmark, would meet the requirements for
a MMF). If cash is not an investment, then "riskless investment" must be an oxymoron, albeit one in widespread use.
Moving on to
Vanguard, that writes: "
Cash investments can lower the overall risk of your portfolio and give you a place to hold money while you
wait to invest it." Vanguard seems to be of two minds - cash is an investment awaiting investment. This is pretty typical. While one may not personally think of cash as an investment, and some in the "actual investing world" agree, it seems others don't (hence the ambiguity).
Much has been made of the fact that Schwab Intelligent Portfolios® (robo investments) have a high allocation to cash. Schwab calls this portion of the portfolio a "
cash investment".
It defends its use of cash on its
FAQ page (see the question "How do you approach cash ..."). There, Schwab says that cash provides stability and liquidity, but also diversification and possible inflation protection. The latter two attributes are usually ascribed to investments.
Finally, TD1 wrote of SRRIX as a "100% non-correlated asset". The meaning in that post was pretty clear and precise, regardless of how sloppily "journalists" might use the term. That's what Maurice was writing about, and what you were responding to when you stated that when everything else was moving up, such a non-correlated asset must necessarily move down (move in the opposite direction).
Likewise, when I wrote "unreliably", I was using it to mean the opposite ("un") of whatever "realiably" meant in the post to which I was responding. Context matters.
